Las medidas de síntesis en estadística son el primer paso que debe darse en el análisis descriptivo y nos proporcionan un resumen cuantitativo del conjunto de datos. Entre las medidas que pueden describir los datos, se comienza por estudiar los valores alrededor de los cuales se agrupa la muestra y la mayor o menor fluctuación alrededor de esos valores. Además, nos interesaremos en ciertos valores que marcan posiciones características de una distribución, así como su simetría y su forma.
De esta forma, las medidas de síntesis de una distribución de frecuencias se clasifican según la posición, dispersión, forma y concentración de los datos.

▫️ Medidas de posición ▫️
Las medidas de posición tratan de resumir y sintetizar el conjunto de datos mediante un valor numérico, si este valor numérico se sitúa hacia el centro de la distribución se habla, entonces, de medidas de posición central. En el caso contrario, nos encontramos ante las medidas de posición no central, las cuales realizan una serie de divisiones iguales en la distribución ordenada de los datos, reflejando los valores superiores, medios e inferiores.
⚠️ Todas las medidas de posición deben verificar que su valor esté comprendido entre el menor y mayor valor del conjunto de datos
Medidas de posición central 1
- Media aritmética, geométrica y armónica: promedio ponderado de los datos, siendo la primera la más utilizada y conocida
- Mediana: valor de la variable que divide a los elementos de la población en dos partes iguales
- Moda: valor que más veces se repite (pueden existir varias modas en una misma distribución)
Medidas de posición no central 2
- Cuartiles: 3 valores de la distribución que dividen la población en cuatro intervalos con igual número de observaciones
- Deciles: 9 valores de la distribución que dividen la población en diez intervalos con igual número de observaciones
- Percentiles: 99 valores de la distribución que dividen la población en cien intervalos con igual número de observaciones
1 En las distribuciones normales, la media aritmética, mediana y moda coinciden. Sin embargo, si la distribución no es normal, entonces la mediana suele estar situada entre la moda y la media aritmética.
2 Los cuartiles, deciles y percentiles medios (Q2, D5 y P50) siempre coinciden con la mediana de la distribución.
▫️ Medidas de dispersión ▫️
Las medidas de dispersión tratan de cuantificar la variabilidad o separación de un conjunto de observaciones, informando acerca de la mayor o menor representatividad de las medidas de posición central.
Medidas de dispersión absoluta
- Rango: diferencia entre el mayor valor y el menor valor de la variable
- Varianza: mide la mayor o menor dispersión de los valores respecto a la media aritmética 3
- Desviación típica: raíz cuadrada de la varianza 4
- Recorrido intercuartílico: diferencia entre el tercer cuartil y el primer cuartil
Medidas de dispersión relativa
- Coeficiente de apertura: cociente entre los 2 valores extremos de una distribución, el cual indica el número de veces que el mayor valor contiene al menor
- Coeficiente de variación de Pearson5: cociente entre la desviación típica y la media aritmética, representando, por tanto, el número de veces que la desviación típica la contiene
3 Cuando la varianza o desviación típica sea próxima a cero, indicará una pequeña dispersión. En caso contrario, si dicha dispersión es muy grande, la media no será representativa.
4 Las unidades de medida de la varianza son exactamente los cuadrados de las unidades de medida de la distribución. Por lo que, se suele utilizar la desviación típica ya que sí posee las mismas unidades de medida.
5 El coeficiente de variación toma valores entre 0 y 1. Si el coeficiente es próximo al 0, significa que existe poca variabilidad en los datos y es una muestra muy compacta. En cambio, si tienden a 1 es una muestra muy dispersa y la media pierde confiabilidad. De hecho, cuando el coeficiente de variación supera el 0,3 se dice que la media es poco representativa.
▫️ Medidas de forma ▫️
Las medidas de simetría y curtosis son denominadas medidas de forma, las cuales permiten cuantificar en lo posible la forma de la distribución de frecuencias. Las medidas de simetría se dirigen a elaborar un indicador que permita establecer el grado de simetría (o asimetría) que presente la distribución, sin necesidad de llevar a cabo su representación gráfica. Y las medidas de curtosis o apuntamiento nos permiten estudiar la concentración central de una distribución, dando lugar a una distribución más o menos apuntada.
⚠️ Todas las medidas de forma deben ser adimensionales
Medidas de simetría 6
- Coeficiente de asimetría de Fisher: coeficiente entre el momento central de orden 3 y el cubo de la desviación típica
- Coeficiente de asimetría de Pearson: coeficiente entre la diferencia de la media y la moda, y la desviación típica
Medidas de curtosis 7
- Coeficiente de curtosis de Fisher: coeficiente entre el momento central de orden 4 y la desviación típica elevada a la cuarta
6 Distribución simétrica (Normal) si el valor del coeficiente es 0; Distribución asimétrica positiva (derecha) si el valor es > 0; Distribución asimétrica negativa (izquierda) si el valor es < 0
7 Distribución mesocúrtica (Normal) si el valor del coeficiente es 0; Distribución leptocúrtica (más apuntada) si el valor es > 0; Distribución platicúrtica (menos apuntada) si el valor es < 0
▫️ Medidas de concentración ▫️
Las medidas de concentración tratan de poner de relieve el mayor o menor grado de igualdad en el reparto del total de los valores de la variable.
- Índice de concentración de Gini: indicador que permite valorar numéricamente la concentración y al mismo tiempo, facilita la comparación entre 2 distribuciones. El valor del coeficiente se encuentra entre 0 y 1, siendo cero la máxima igualdad y mínima concentración. Mientras que, 1 expresa la máxima desigualdad y la máxima concentración
- Curva de Lorenz: representación gráfica utilizada frecuentemente para plasmar la distribución relativa de una variable en un dominio determinado. Cada punto de la curva se lee como porcentaje acumulativo de las variables. Cuanto mayor sea el área que queda entre la recta y la curva, mayor será la desigualdad existente
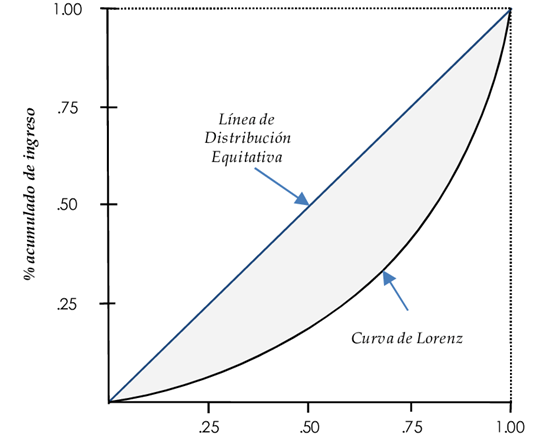
⚠️ Dos distribuciones pueden tener el mismo grado de concentración (Índice de Gini igual), pero la representación de las curvas de Lorenz sea distinta, es decir, la estructura del reparto no sea la misma
Si te ha parecido interesante, ¡compártelo y síguenos también en todas nuestras redes sociales!
Publicado el 12 de septiembre de 2023