La cantidad de información que procesamos día a día es enorme. Como seres racionales y analíticos que somos, tendemos a buscar vínculos entre los datos para obtener conclusiones y predicciones a partir de ellos. Estos vínculos se logran mediante la exploración de relaciones estadísticas entre variables, principalmente a través de la regresión y la correlación.
🔎 Representación gráfica
El primer paso para identificar algún tipo de tendencia entre las variables es realizar una representación gráfica de los datos. Para ello utilizamos el diagrama de dispersión, el cual es parecido al juego de hundir la flota.
Cada observación tiene dos coordenadas: coordenada X y coordenada Y. El punto que representa a esa observación se ubica en la intersección de las dos coordenadas. Debemos tener en cuenta que los diagramas de dispersión muestran posibles asociaciones o relaciones entre las variables, pero puede no existir una relación causa y efecto.
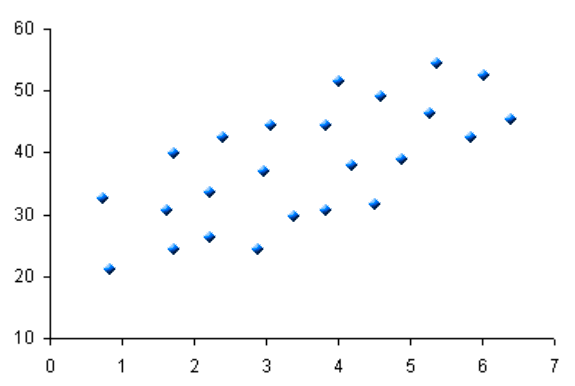
Para interpretar una diagrama de este tipo hay que buscar tendencias en los datos de izquierda a derecha. Si los datos muestran una tendencia ascendente, significa que puede existir una relación positiva entre X e Y (a medida que aumentan los valores de X, también aumentan los de Y). Si los datos muestran una tendencia descendente, significa que puede existir una relación negativa entre X e Y (a medida que aumentan los valores de X, disminuyen los de Y). Por el contrario, si los datos no parecen revelar ninguna tendencia, entonces puede no existir ninguna relación entre X e Y.
〰️ Regresión
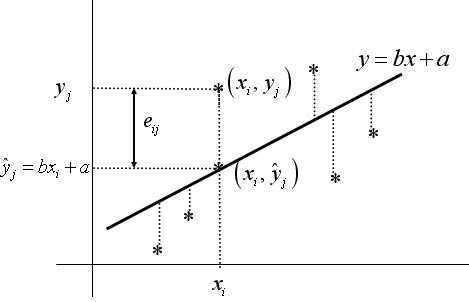
Si se ha establecido algún tipo de tendencia mediante el diagrama de dispersión, el siguiente paso consiste en la búsqueda de una función que exprese lo mejor posible el tipo de relación entre las variables. El caso más frecuente es la relación funcional entre las variables mediante una recta (y = bx + a), es decir, estamos hablando de la regresión lineal entre X e Y.
Una de las aplicaciones más interesante que tiene la regresión es la de predecir: conocido el valor de una de las variables, estimar el valor que presentará la otra variable relacionada con ella. Así, se determina entre todas las rectas que tienen como ecuación general, aquella que, mejor se ajusta a la nube de puntos de la distribución bidimensional según el procedimiento de Mínimos Cuadrados.
La recta de mejor ajuste es y = mx + b, donde m es la pendiente de la recta (cociente en la variación de Y y la variación de X) y b es el punto de intersección con el eje Y (donde el valor de x es cero). Para encontrar esta recta, debemos encontrar los valores de m y b que mejor ajusten la tendencia de los datos.
De esta forma, la recta de regresión de Y sobre X es:
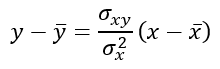
Y la recta de regresión de X sobre Y:
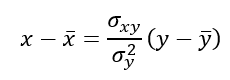
🔗 Correlación
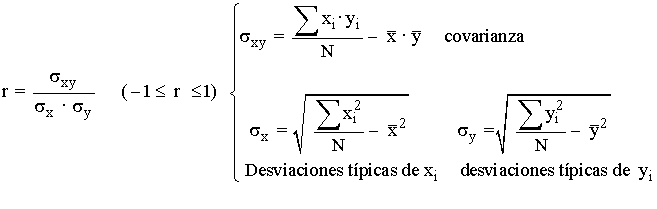
Una vez identificado el vínculo de las variables mediante el diagrama de dispersión y la regresión, el último paso es obtener un estadístico que cuantifique o mida el alcance de la relación. El más utilizado es el coeficiente de correlación lineal de Pearson (r), el cual indica la dependencia lineal que existe entre dos variables a través de su covarianza y sus desviaciones típicas.
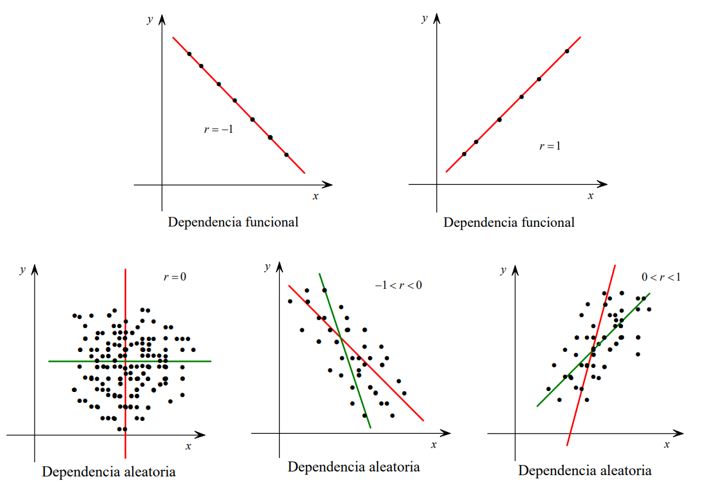
Los posibles resultados del coeficiente varían entre -1 y 1. En estos 5 gráficos se pueden observar las posiciones que adopta la recta de regresión y el diagrama de puntos según el valor de r.
Si r = 1 existe una correlación perfecta positiva, es decir, las variables crecen en el mismo sentido. Si r = -1 existe una correlación perfecta negativa, es decir, las variables crecen en sentido opuesto. Cuando r = 0 la correlación lineal es nula, es decir, las variables no están relacionadas. Si -1 < r < 0 existe cierto grado de correlación negativa (mayor cuanto más próximo a -1). Y por último, si 0 < r < 1 existe cierto grado de correlación positiva (mayor cuanto más próximo a 1).
⚠️ Atención: en caso de estudiar en primer lugar la correlación entre las variables, debemos obtener unos valores de r superiores a +0.5 o inferiores a -0.5 para poder llevar a cabo posteriormente un buen análisis de regresión.
Si te han parecido interesante este post sobre los vínculos entre los datos, ¡compártelo y síguenos también en todas nuestras redes sociales!
Publicado el 3 de mayo de 2022