¿Qué técnica utilizar para analizar tus datos?

Una de las preguntas más frecuentes que recibimos en LETSTAT es: “Tengo datos, pero… ¿qué análisis debo hacer?”

Y es completamente normal. Hoy en día existen muchísimas técnicas estadísticas, y elegir la adecuada no depende solo de “lo que esté de moda”, sino de tu objetivo, tu tipo de variables y la calidad de tus datos. En este post te damos una guía clara y práctica para saber qué técnica utilizar para analizar tus datos, según tu caso.

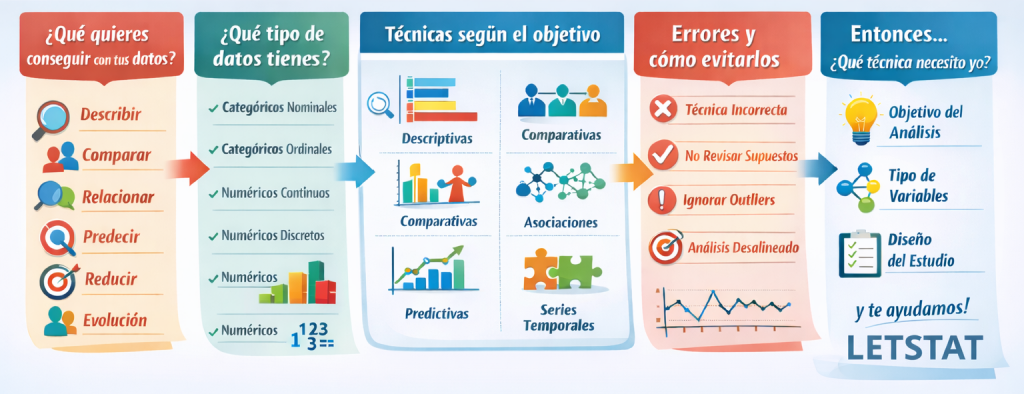
1. ¿Qué quieres conseguir con tus datos?

La técnica correcta nace de la pregunta correcta. Antes de pensar en el software o en el modelo, conviene responder a esto:

• ¿Quieres describir una muestra?
• ¿Quieres comparar grupos?
• ¿Quieres ver relaciones entre variables?
• ¿Quieres predecir un resultado?
• ¿Quieres reducir dimensiones o crear perfiles?
• ¿Quieres analizar evolución temporal?

2. ¿Qué tipo de datos tienes?

En estadística, no se analiza igual una variable “edad” que una escala tipo Likert o una categoría como “sexo”. Clasificación de tipos de variables más comunes:

• Categóricas nominales: son variables que representan categorías sin orden natural. Sirven para clasificar en grupos diferentes, pero no tiene sentido decir que una categoría es “mayor” o “mejor” que otra. Ejemplos: sexo, provincia, tipo de tratamiento.
• Categóricas ordinales: son variables con categorías ordenadas, donde sí existe una jerarquía (de menor a mayor), pero no podemos asegurar que la distancia entre categorías sea la misma. Ejemplos: escalas de satisfacción, Likert (1–5).
• Numéricas continuas: son variables cuantitativas que pueden tomar infinitos valores dentro de un rango, incluyendo decimales. Se miden en una escala numérica real. Ejemplos: peso, ingresos, puntuaciones clínicas.
• Numéricas discretas: son variables cuantitativas que toman valores enteros y contables, es decir, se obtienen al contar elementos y no suelen tener decimales. Ejemplos: número de visitas, número de hijos.

3. Técnicas recomendadas según el objetivo del análisis

3.1. Si quieres describir tus datos

Útil si estás en una fase exploratoria o de “fotografía” del dataset. Ideal para informes iniciales, tesis o artículos donde hay que caracterizar la muestra. Técnicas típicas descriptivas:

• Tablas de frecuencias y porcentajes
• Medias, medianas, desviación típica, rango intercuartílico
• Gráficos (barras, histogramas, boxplots)

3.2. Si quieres comparar grupos

Este tipo de análisis es uno de los más habituales en investigación (clínica, educación, psicología, turismo, marketing…), ya que permite comprobar si existen diferencias significativas entre dos o más grupos de personas, condiciones o momentos. Ejemplos de preguntas: ¿Hay diferencias entre hombres y mujeres? ¿Cambian los resultados antes y después de una intervención? ¿Se comportan distinto varios grupos?

Técnicas habituales inferenciales:

• t de Student (variable dependiente cuantitativa; independencia de observaciones; normalidad por grupo; homogeneidad de varianzas —si no, t de Welch).
• ANOVA (variable dependiente cuantitativa; independencia; normalidad de residuos; homogeneidad de varianzas).
• Mann–Whitney / Wilcoxon (datos ordinales o cuantitativos; independencia; no requiere normalidad; recomendable distribución similar si se interpreta como diferencia de tendencia central).
• Kruskal–Wallis (ordinal o cuantitativa; independencia; no requiere normalidad; recomendable distribución similar entre grupos).
• Chi-cuadrado (variables categóricas; independencia; frecuencias esperadas suficientes —si son bajas, mejor Fisher).

Importante: uno de los errores más comunes es aplicar pruebas paramétricas (como la t de Student) sin comprobar previamente los supuestos (especialmente normalidad y homogeneidad de varianzas) o utilizarlas con variables que no lo permiten. Elegir bien el test marca la diferencia entre un resultado fiable… y uno engañoso.

3.3. Si quieres estudiar relaciones o asociaciones

Este tipo de análisis se utiliza cuando tu objetivo es comprobar si existe una relación estadística entre dos variables, es decir, si cuando una cambia, la otra tiende a cambiar también (en el mismo sentido o en sentido contrario). No se trata necesariamente de demostrar causa-efecto, sino de identificar patrones de asociación que puedan ser relevantes para tu investigación. Técnicas comunes:

• Correlación de Pearson (cuando ambas variables son numéricas y se busca una relación lineal; recomendable si se cumplen supuestos como normalidad aproximada y ausencia de valores extremos influyentes).
• Correlación de Spearman (cuando las variables son ordinales, o cuando no se cumplen supuestos para Pearson; detecta relaciones monótonas, no necesariamente lineales).
• Tablas cruzadas + Chi-cuadrado (cuando ambas variables son categóricas y quieres comprobar si están asociadas, por ejemplo, si la distribución de una variable cambia según la otra).
• V de Cramer (se utiliza como medida complementaria al Chi-cuadrado para cuantificar la intensidad de la asociación entre variables categóricas).

Importante: que dos variables estén correlacionadas no implica causalidad. Sin embargo, encontrar asociaciones relevantes puede ser el primer paso para plantear modelos más completos o análisis explicativos posteriores.

3.4. Si quieres explicar o predecir un resultado

Cuando ya no solo quieres “ver diferencias” o “ver relaciones”, sino entender qué factores influyen en un resultado o incluso anticiparlo, necesitas trabajar con modelos estadísticos. Este enfoque es especialmente útil en artículos científicos y proyectos aplicados porque permite analizar varias variables a la vez y obtener conclusiones más sólidas.

Según el tipo de variable dependiente (lo que quieres explicar o predecir):

• Resultado continuo → Regresión lineal (por ejemplo, predecir una puntuación, un gasto medio o un valor clínico).
• Resultado sí/no → Regresión logística (por ejemplo, predecir probabilidad de “abandona/no abandona”, “enfermedad sí/no”).
• Resultado ordinal → Regresión ordinal (por ejemplo, niveles de satisfacción: baja/media/alta).
• Resultado de conteo → Poisson / Binomial negativa (por ejemplo, número de visitas, número de incidencias, número de compras).
• Tiempo hasta un evento → Análisis de supervivencia (Kaplan–Meier, modelo de Cox; por ejemplo, tiempo hasta recaída, tiempo hasta erupción, tiempo hasta abandono).

¿Qué ventajas aportan estos modelos?

• Controlar variables (por ejemplo, ajustar por edad, sexo u otros factores para evitar confusión).
• Estimar efectos (cuánto cambia el resultado si cambia una variable, con intervalos de confianza).
• Hacer predicción (estimar probabilidades o valores esperados en nuevos casos).

3.5. Si quieres reducir muchas variables o detectar estructura

Cuando trabajas con cuestionarios largos o bases con muchos indicadores, analizar variable por variable puede ser poco eficiente y difícil de interpretar. En estos casos interesa descubrir si existe una estructura interna: dimensiones comunes, patrones o componentes que resuman la información. Técnicas más comunes:

• PCA (Análisis de Componentes Principales): reduce la información a un número pequeño de componentes, ideal para construir índices compuestos o rankings.
• Análisis Factorial Exploratorio (AFE): identifica factores latentes (constructos) detrás de un conjunto de ítems, muy útil en cuestionarios.
• Análisis Factorial Confirmatorio (AFC): se usa cuando ya existe una estructura teórica previa y quieres confirmar si el modelo encaja con tus datos.

Muy usado en validación de cuestionarios, construcción de índices (competitividad, calidad, satisfacción) e investigación en ciencias sociales y salud.

3.6. Si quieres segmentar perfiles o agrupar casos

Este enfoque se utiliza cuando tu objetivo es identificar tipologías o perfiles dentro de una muestra: grupos de personas similares entre sí y diferentes de otros grupos. Es muy habitual en turismo, marketing, comportamiento del consumidor, educación o investigación social. Técnicas habituales:

• Clúster jerárquico (muy útil para explorar y decidir cuántos grupos existen).
• k-medias (funciona bien cuando las variables son numéricas y comparables).
• Clases latentes (enfoque probabilístico, útil para perfiles “no observables” directamente).
• ACM + clúster (especialmente recomendado cuando hay muchas variables categóricas/encuestas).

3.7. Si tus datos son temporales (series temporales)

Cuando tus datos están organizados por meses, trimestres o años, no basta con aplicar técnicas “estándar”, porque los valores suelen estar relacionados con el tiempo (tendencias, estacionalidad, dependencia entre observaciones). Aquí el objetivo suele ser analizar la evolución, detectar cambios o hacer predicción. Técnicas comunes:

• Descomposición de series (separar tendencia, estacionalidad y componente irregular).
• Modelos ARIMA/SARIMA (predicción de series con o sin estacionalidad).
• Pruebas de raíz unitaria (ADF) (comprobar estacionariedad).
• Cointegración (Johansen) (relaciones de equilibrio a largo plazo entre series).
• Causalidad de Granger (si una serie ayuda a predecir a otra).

Importante: en series temporales es fácil encontrar “relaciones falsas” si no se controla la tendencia o la dependencia temporal.

4. Errores típicos al elegir una técnica y cómo evitarlos

• Elegir el análisis “porque lo vi en otro artículo” (sin validar si aplica a tu caso).
• No revisar supuestos (normalidad, homocedasticidad, independencia, etc.).
• Analizar escalas tipo Likert como continuas sin justificarlo.
• No tratar valores perdidos o datos atípicos (outliers).
• No alinear el análisis con el objetivo del estudio (la técnica no responde a la pregunta).

5. Entonces… ¿qué técnica necesito yo?

Para recomendar una técnica adecuada, en LETSTAT normalmente pedimos tres cosas:

1. Objetivo del análisis (qué quieres responder o demostrar)
2. Tipo de variables (dependiente e independientes)
3. Diseño del estudio (grupos, repetidas, longitudinal, experimental, observacional…)

¿Quieres que te ayudemos a elegir el análisis adecuado?

En LETSTAT te ayudamos a elegir la técnica correcta según tu objetivo, analizar tus datos con rigor, interpretar resultados y redactarlos correctamente y, preparar informes, tablas y figuras para publicaciones.

📩 Contáctanos y cuéntanos tu caso. Te orientamos sin compromiso.